LAPORAN PRAKTIKUM FISIKA DASAR: “BANDUL MATEMATIS”

LAPORAN PRAKTIKUM

FISIKA DASAR

“BANDUL MATEMATIS”

O

L

E

H

NAMA                        : FATMA ZAHRA

NO BP.            : 1404045

KELAS           : A

SEKOLAH TINGGI FARMASI INDONESIA

YAYASAN PERINTIS

PADANG 2014

BANDUL MATEMATIS

I.                   TUJUAN

a.       Mengetahui hubungan antara periode bandul matematis dengan panjang tali gantungan

b.      Menentukan percepatan gravitasi suatu tempat.

II.                TEORI DASAR

Berat adalah gaya tarik bumi terhadap benda. Percepatan gravitasi (g) adalah percepatan yang dialami oleh benda kerena beratnya sendiri. Menurut hukum newton II gaya  F=ma .Dalam hal ini gaya berat benda F=mg.

Beban yang diikat pada ujung tali ringan yang massanya dapat diabaikan disebut bandul. Bandul Matematis adalah salah satu matematis yangbergerak mengikuti gerak harmonik sederhana. bandul matematis merupakan benda ideal yang terdiri dari sebuah titik massa yang digantungkan pada tali ringan yang tidak bermassa. jika bandul disimpangkan dengan sudut θ dari posisi setimbangnya lalu dilepaskan maka bandul akan berayun pada bidang vertikal karena pengaruh dari gaya grafitasinya.

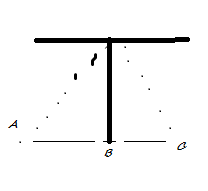
Prinsip Ayunan yaitu Jika sebuah benda yang digantungkan pada seutas tali, diberikan simpangan, lalu dilepaskan, maka benda itu akan berauyn kekanan dan ke kiri. Berarti ketika benda berada disebelah kiri akan dipercepat kekanan, dan ketika benda sudah ada disebelah kanan akan diperlambat dan berhenti, lalu dipercepat kekiri dan seterusnya. Dari gerakan ini dilihat bahwa benda mengalami percepatan selama gerakan nya. Menurut hukum Newton (F = m.a) percepan hanya timbul ketika ada gaya. Arah percepatan dan arah gaya selalu sama.

Ketika beban digantungkan pada ayunan dan tidak diberikan gaya maka benda akan diam di titik kesetimbangan B. Jika beban ditarik ke titik A dan dilepaskan, maka beban akan bergerak ke B, C, lalu kembali lagi ke A. Gerakan beban akan terjadi berulang secara periodik, dengan kata lain beban pada ayunan di atas melakukan gerak harmonik sederhana.

Pada contoh di atas, benda mulai bergerak dari titik A lalu ke titik B, titik C dan kembali lagi ke B dan A. Urutannya adalah A-B-C-B-A. Seandainya benda dilepaskan dari titik C maka urutan gerakannya adalah C-B-A-B-C.

jika beban ditarik kesatu sisi, kemudian dilepaskanmaka beban akan terayun melalui titik keseimbangan menuju ke sisi yang lain. Bila amplitudo ayunan kecil, maka bandul sederhana itu akan melakukan getaran harmonik. Bandul dengan massa m digantung pada seutas tali yang panjangnya l. Ayunan mempunyai simpangan anguler θ dari kedudukan seimbang. Gaya pemulih adalah komponen gaya tegak lurus tali.
F = - m g sin θ
F = m a
maka
m a = - m g sin θ
a = - g sin θ

Untuk getaran selaras θ kecil sekali sehingga sin θ = θ. Simpangan busur s = l θ atau θ=s/l , maka persamaan menjadi: a= gs/l . Dengan persamaan periode getaran harmonic:

G = 4 π² L / T²  

T= t/n

Dimana :
l = panjang tali (meter)
G= percepatan gravitasi (ms-2)
T= periode bandul sederhana (s)

Dari rumus di atas diketahui bahwa periode bandul sederhana tidak bergantung pada massa dan simpangan bandul, melaikan hanya bergantung pada panjang dan percepatan gravitasi

Osilasi adalah jika suatu partikel dalam gerak periodik bergerak bolak balik melalui lintasan yang sama, dimana suatu periodik adalah setiap gerak yang berulang-ulang dalam selang waktu yang sama. Banyak benda yang berisolasi yang bergerak  bolak-baliknya tidak tepat sama karena gaya gesekan melepaskan tenaga geraknya. Bandul matematis bergerak mengikuti gerak harmonic. Bandul sederhana (matematis) adalah benda ideal yang terdiri dari sebuah titik massa, yang digantung pada tali ringan yang tidak dapat muju. Jika bandul ditarik keseamping dari posisi seimbangnya (David, 1985 : 12)

Banyak benda yang berosilasi bergerak bolak-balik tidak tepat sama karena gaya gesekan melepaskan tenaga geraknya.

syarat untuk mendapat osilasi atau ayunan :

-a. Gaya yang selalu melawan arah simpangan dari suatu posisi seimbang. Dalam hal ini gaya yang melawan simpangan adalah gaya tangensial.

b. Kelembaman yang memebuat benda tak berhenti ketika dalam posisi yang seimbangan (tampa gaya). Dalam contoh ini massa yang berayun tidak berhenti tetapi pada posisi bawah (posisi tengan, gaya nol), tetapi bergerak terus karena kelembaman massanya.

Periode T suatu gerak harmonik adalah waktu yang dibutuhkan untuk menempuh suatu lintasan langkah dari geraknya yaitu satu putaran penuh atau satu putar frekwensi gerak adalah V=1/T .

Satuan SI untuk frekwensi adalah putaran periodik hert. posisi pada saat tidak ada gaya netto yang bekerja pada partikel yang berosilasi adalah posisi setimbang. partikel yang mengalami gerak harmonik bergerak bolak-balik melalui titik yang tenaga potensialnya minimum (setimbang). Benda dikatakan melakukan satu getaran jika benda bergerak dari titik di mana benda tersebut mulai bergerak dan kembali lagi ke titik tersebut. Satuan periode adalah sekon atau detik.contoh bandul berayun. Amplitudo adalah pengukuran scalar yang non negative dari besar osilasi suatu gelombang. Amplitudo juga dapat didefinisikan sebagai jarak terjatuh dari garis kesetimbangan dalam gelombang sinusoide yang kita pelajari pada mata pelajaran fisika dan matematika.

Pada bandul metematis, periode dan frekuensi sudut pada bandul sederhana tidak tergantung pada masa bandul, tetapi bergantung pada panjang tali dan percepatan gravitasi setempat.

Jika L dan T diukur, maka maka harga g dapat dihitung. Ketelitian harga g dapat terpenuhi jika:

1.      Massa tali lebih kecil dibandingkan masa benda

2.      Simpangan harus lebih kecil

3.      Gerakan –gerakan dengan udara luar kecil, sehingga dapat diabaikan

4.      Gaya torsi (putaran) harus tidak ada, benda berayun dalam satu bidang.

III.             ALAT-ALAT YANG DIGUNAKAN

1.      Benda logam

2.      Benang

3.      Tali panjang

4.      Stopwach

5.      Jangka sorong

IV.             PROSEDUR KERJA

1.      Gantung sampul dengan tali simpul, hingga panjang sampai pada pusat bandul.

2.      Ayun bandul dengan sudut kecil sekitar 10 ⁰

3.      Hitung waktu untuk 25 kali ayuanan dengan stopwatch , ulangi percobaan ini sebanyak 3 kali.

4.      Berturut-turut ubahlah panjang tali men jadi L2, L3, L4 dan seterusnya, lakukan  percobaan 2 dan 3 kembali.

5.      Buat grafik antara L dan T dan apa kesimpulan saudara

6.      Dari pengamatan, carilah harga percepatan gravitasi.

V.                HASIL DAN PEMBAHASAN

a.       Hasil

1.      L ₁ =46 cm = 0,46 m

T= t/n = 34/25 = 1,36 s

T²⁼  (1,36)²  = 1,84 S

G = 4 π² L / T² = 4x9,8596x0,46/1,84 = 9,8 m/s²

2.      L ₂ = 41 cm = 0,41 m

T = t/n = 32,13/ 25= 1,28 s

T ² = (1,28)2 = 1,64 s

G= 4πr²L/T² = 4x9,8596x0,41/1,64= 9,85 m/s²

3.      L ₃ = 36 cm = 0,36 m

T = t/n = 30/ 25= 1,2 s

T ² = (1,2)2 = 1,44 s

G= 4πr²L/T² = 4x9,8596x0,36/1,44= 9,8596 m/s²

4.      L ₄ = 32 cm = 0,32 m

T = t/n = 28,8/ 25= 1,15 s

T ² = (1,15)2 = 1,32 s

G= 4πr²L/T² = 4x9,8596x0,32/1,32= 9,5 m/s²

5.      L ₅ = 2,85 cm = 0,285 m

T = t/n = 26,73/ 25= 1,06 s

T ² = (1,06)2 = 1,13 s

G= 4πr²L/T² = 4x9,8596x0,825/1,18= 9,946 m/s²

6.      L ₆ = 23,5 cm = 0,235 m

T = t/n = 24,66/ 25= 0,98 s

T ² = (0,98)2 = 0,96 s

G= 4πr²L/T² = 4x9,8596x0,235/0,96= 9,65 m/s²

7.      L ₇ = 185 cm = 0,185 m

T = t/n = 2,22/ 25= 0,88 s

T ² = (0,88)2 = 0,78 s

G= 4πr²L/T² = 4x9,8596x0,185/0,78= 9,375 m/s²

8.      L ₈ = 14 cm = 0,14 m

T = t/n = 19,71/ 25= 0,78 s

T ² = (0,78)2 = 0,61 s

G= 4πr²L/T² = 4x9,8596x0,14/0,61= 9,05 m/s²

9.      L ₉ = 9 cm = 0,09 m

T = t/n = 15,48/ 25= 0,65 s

T ² = (0,65)2 = 0,37 s

G= 4πr²L/T² = 4x9,8596x0,09²/0,37= 9,5 m/s²

10.  L ₁₀ = 4 cm = 0,04 m

T = t/n = 10/ 25= 0,4 s

T ² = (0,4)2 = 0,16 s

G= 4πr²L/T² = 4x9,8596x0,04/0,16= 9,85 m/s²

Tabel percobaan bandul matematis’

No	Panjang (m)	T (s)	T2 (s)	G (m/s2)
1	L1=0,46	1,36	1,84	9,8
2	L2=0,41	1,28	1,64	9,85
3	L3=0,36	1,2	1,44	9,8596
4	L4=0,32	1,15	1,32	9,5
5	L5=0,285	1,06	1,13	9,946
6	L6=0,235	0,98	0,96	9,65
7	L7=0,185	0,88	0,78	9,375
8	L8=0,4	0,78	0,61	9,05
9	L9=0,09	0,65	0,37	9,5
10	L10=0,04	0,4	0,16	9,85

b.      Pembahasan

Pada percobaan ini kami mengukur panjang tali terlebih dahulu, setelah didapat, kami mencaroi nilai periode bandul dengan rumus:

T=t/n

Selanjutnya T yang didapat kemudian dikuadratkan, setelah didapat hasil baru dicari percepatan gravitasa bandul dengan rumus:

G= 4πr²L/T²

Dari 10 percobaan yang telah dilakukan, ternyata hanya 5 percobaan yang hasilnya sesuai dengan teori, yaitu yang percepatan gravitasinya berkisar antara 9,8-10 m/s². Sedangkan yang lainnya tidak. Adanya perbedaan percepatan gravitasi tersebut dipengaruhi oleh gaya torsi, banyak ayunan bergetar, waktu, dan faktor angin.

VI.             KESIMPULAN DAN SARAN

a.       Kesimpulan

1.      Berdasarkan rumus T=2π p/^----L/g. diketahui bahwa periode (T) berbanding lurus dengan akar panjang bandul (L)

2.      Berdasarkan hasil percobaan ternyata hanya 5 percobaan yang hasilnya sesuai dengan teori, yaitu yang percepatan gravitasinya berkisar antara 9,8-10 m/s². Sedangkan yang lainnya tidak. Adanya perbedaan percepatan gravitasi tersebut dipengaruhi oleh gaya torsi, banyak ayunan bergetar, waktu, dan faktor angin.

b.      Saran

Sebaiknya melakukan percobaan secara berulang-ulang, karena jika hanya melakukan satu kali percobaan , tingkat ketepatannta akan berkurang. Percobaan harus teliti dan cermat dalam mengamati waktu dan menghitung getaran yang terjadi, karena akan berpengaruh pada periode yang dihasilkan. Jika dalam perhitungan periode terjadi kesalahan , maka akan berpengaruh terhadap besarnya percepatan gravitasi.

DAFTAR PUSTAKA

Bakti, S. 2007. Desain Instrument Elektronik untuk Mengukur Gravitasi Muatan dengan Prinsip Bandul matematis. Mataram: Gravity

Giancoli, D . 2007. Fisika. Jakarta: Erlangga

Halliday.2005. Fisika dasar. Jakarta: Erlangga

Tripler, Paul A. 1991. Fisika untuk Sains dan Teknik Edisi ke III Jilid 2 .      Jakarata: erlangga